逆に,2つの三角形が相似であるとき,次の (1) (2) (3)はすべて成り立つ. 要点 (1) 2組の角がそれぞれ等しい (2) 3組の辺の比がそれぞれ等しい (3) 2組の辺の比とその間の角がそれぞれ等しい (解説) (1) 三角形の内角の和は180°だから「2組の角がそれぞれ等しい」とき,「3組の角がそれぞれ等しくなる」 相似であることを証明するには「2組」を示せば十分だと〇相似な図形の対応する辺,角,頂点を それぞれ指摘することができる。 〇相似な図形の性質を理解している。 数学的技能 主体性 ・観察 ・プリント ・発表 情 報 収 集 三 解 べ 2 と 角形の 相似 条件を理 し,図形の性質を調 たり,距離や高さを こんにちは。和からの数学講師の岡本です。前回に引き続き、フラクタル図形のテーマでお話ししていきます。前回の内容のマスログはこちら。 今回は自己相似性と次元についてのお話です。 フラクタルってなに?~その特徴と歴史その①~ 1.自己相似性 自
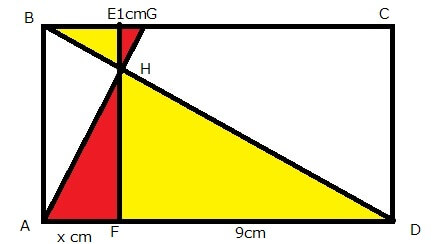
開成中学入試問題 算数 を徹底解説 平成29年度 算数 大問3 1 相似の図形ー第2回 星一徹式ゲリラ中学受験
図形と相似 面積比
図形と相似 面積比- 相似な関係にある2つの平面図形の相似比がa:bの場合、面積比はa 2 :b 2 になる という性質があります。 これがおぼえるべき、2つ目の型です。 さきほど示した17種類の内、14個は①と②をベースにしたものです。・ 相似の概念を明らかにし、2つの相似な図形を観察して、相似な図形の性質を考えること ができる。 ・ 相似の意味、性質、相似比について理解する。



相似とは 三角形の相似条件 記号 相似比 面積比 証明問題 受験辞典
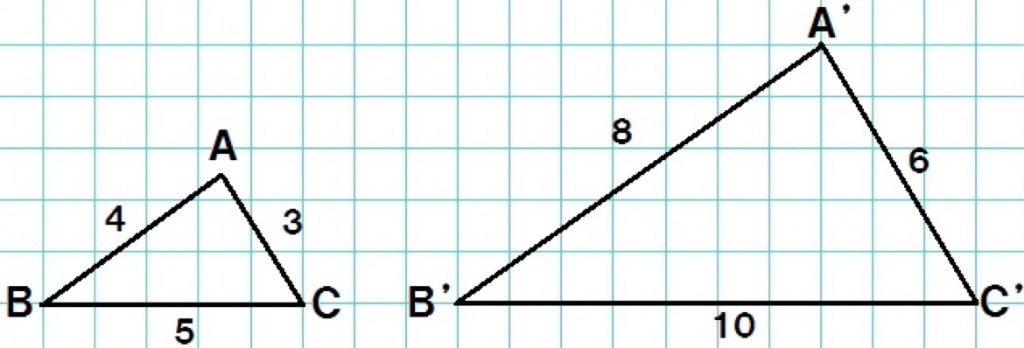
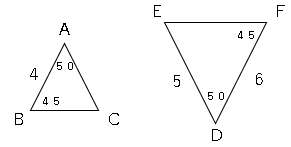
相似な図形の相似比と面積比及び体積比を調べ、文字式を用いるなどしてそれらの関係 について考えることができる。 数学的な技能 ある図形の面積がわかっているとき、その図形の面積や体積を相似比をもとにして求め ることができる。 数量や図形などにつこの3つの中から相似な図形を見つけるときに 情報が少ない図形は、相似条件に当てはめることができません。 なので、情報が多く揃っている ABCと ABDが相似になるだろうな、と予想して この2つの三角形が、相似条件に当てはまるかを確かめていきます。 どれが相似な図形なのか判断がつきにくいときは 辺の長さや角の大きさが、たくさんわかっている図形に相似な図形の相似比を求めることができる。 相似な図形の対応する辺の比やとなり合 う辺の比が等しいことを使って求めるこ とができる。 (ノート・振り返り) ・三角形の相似条件 を理解し,三角形の (2) 三角形の相似条件を理解している。
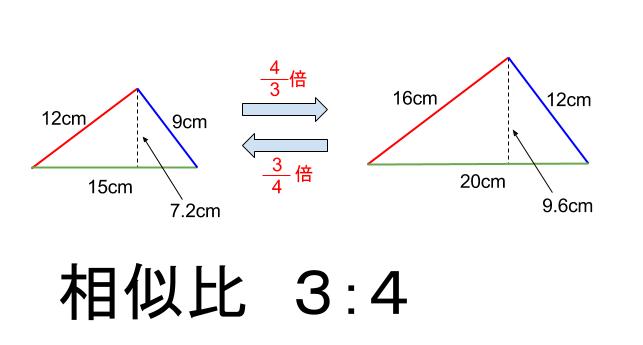
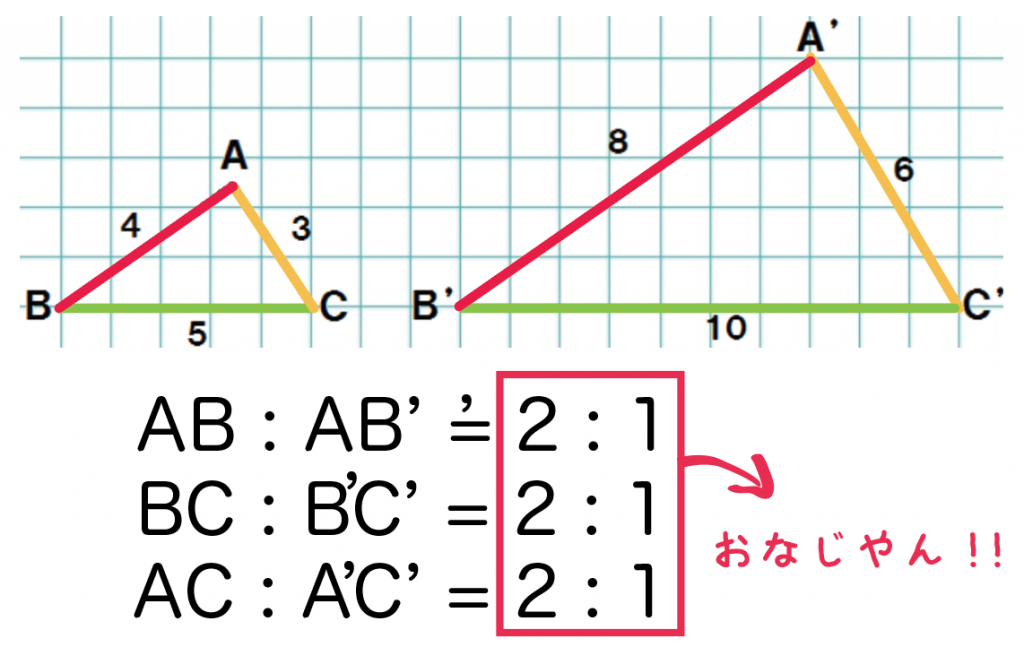
そこで,図形と相似の導入で以下の点に留意しながら授業実践を行った。 尚,この記録は前任校の東金市立北中学校で実践したものである ・パズル的な作業学習を取り入れる事で,苦手意識をもっている生徒も意欲をもって活動できるようにする。 ・少人数のグループ学習の形を取る事により,多くの生徒に活躍する場面を与えたり,教え合いを通して理解を深め1 1 BASICで描く自己相似図形 11 自己相似図形 111 相似縮小変換と自己相似図形 相似縮小変換f 1 , f 2 に対して, f 1(D)∪f 2(D) = D となる図形D を自己相似図形といいま す。Dは有界であるものと仮定すれば,D を描く手続きを次のように作成することで,D を 描くことができます。 相似の場合、対応する辺の比は全部同じです。「相似比」と呼ばれますが、上の画像にある三角形の場合は abcと defの相似比は、 abc: def= 12になります。 違いを理解して、言い回
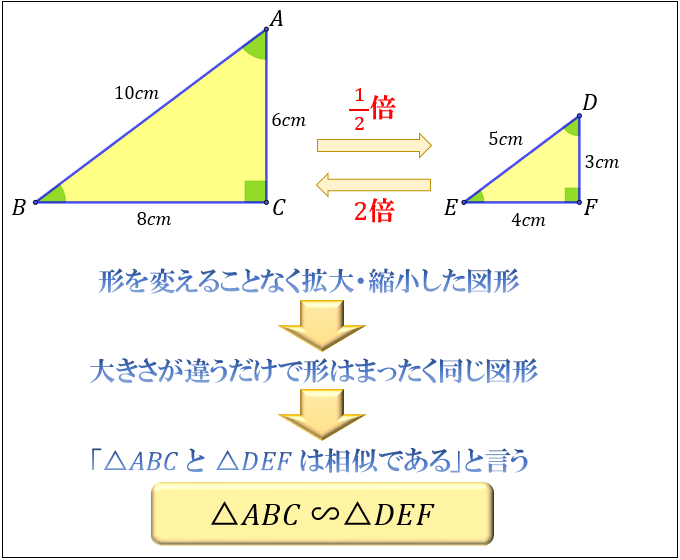
相似な図形の面積比と体積比 相似な図形の面積比は相似比の2乗に等しく、相似な図形の体積比は相似の3乗に等しい。 \(相似比 \quad mn \quad \to \quad 面積比 \quad m^2n^2 \quad \to \quad 体積比 \quad m^3n^3 \)<相似の定義> 1つの図形を,形を変えずに一定の割合に拡大,または縮小して得られる図形は,もと の図形と相似である。 <相似な図形の性質> 相似な図形では,対応する部分の長さの比はすべて等しく,対応する角の大きさはそれ ぞれ等しい。相似比の解説 ある図形を拡大もしくは縮小した図形のことを相似な図形と言います。 相似な図形には以下のような特徴があります。 ・対応する辺の長さの比は全て等しい ・対応する角度はそれぞれ等しい 相似比




相似な図形の面積比の問題 相似比を出してから二乗しよう 中学や高校の数学の計算問題




図形の相似 Wikipedia
図形が相似なら 「線関係」 → 「そのまま相似比」 「面積関係」 → 「2乗 (平方)」 「体積関係」 → 「3乗 (立方)」 ですね →④相似な図形の相似比と面積 比及び体積比に関心をもち,そ れらの関係について考えよう としている。 ⑤相似な図形の性質を用いて 具体的な事象を捉えることに 関心をもち,問題の解決に生か そうとしている。 ①相似な図形の性質を見いだ すことが数学35章図形と相似「相似な図形」<準備問題①> 組 番 名前 1三角形の合同条件を書きなさい。 2次の図で,AB//CDのとき,次の問いに答えなさい。



1
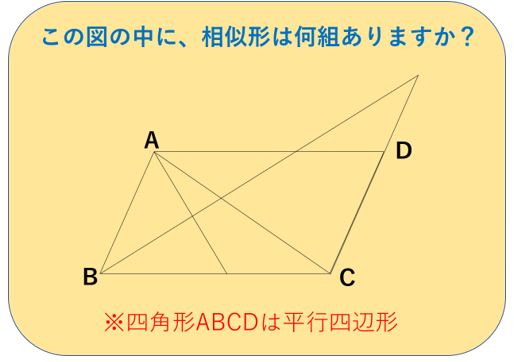



平面図形と比 相似形を探してみよう 中学受験プロ講師ブログ
図形と相似 Try IT(トライイット)の図形の相似の問題の様々な問題を解説した映像授業一覧ページです。 図形の相似の問題を探している人や問題の解き方がわからない人は、単元を選んで問題と解説の映像授業をご覧ください。 相似比と面積比,体積比の公式の証明 レベル ★ 基礎 平面図形 更新日時 相似な平面図形について,面積比=相似比の二乗 相似な空間図形について,体積比=相似比の三乗 面積比をきちんと理解できれば体積比もほぼ同様に理解できるので中学3年生 数学 相似な図形 練習問題プリント 無料ダウンロード・印刷 相似な図形のかき方、三角形の相似条件や、相似を利用した距離や高さの求め方を練習していきます。
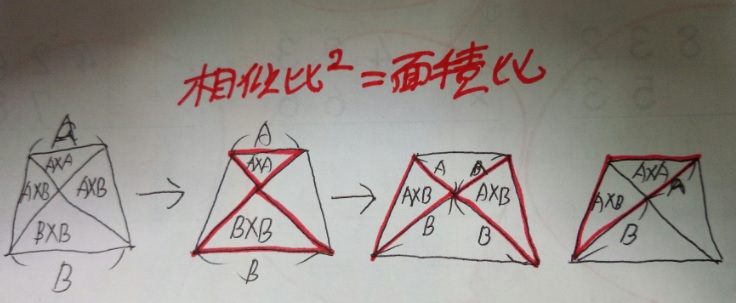



面積比と相似 図形の面積比は相似比の2乗 中学
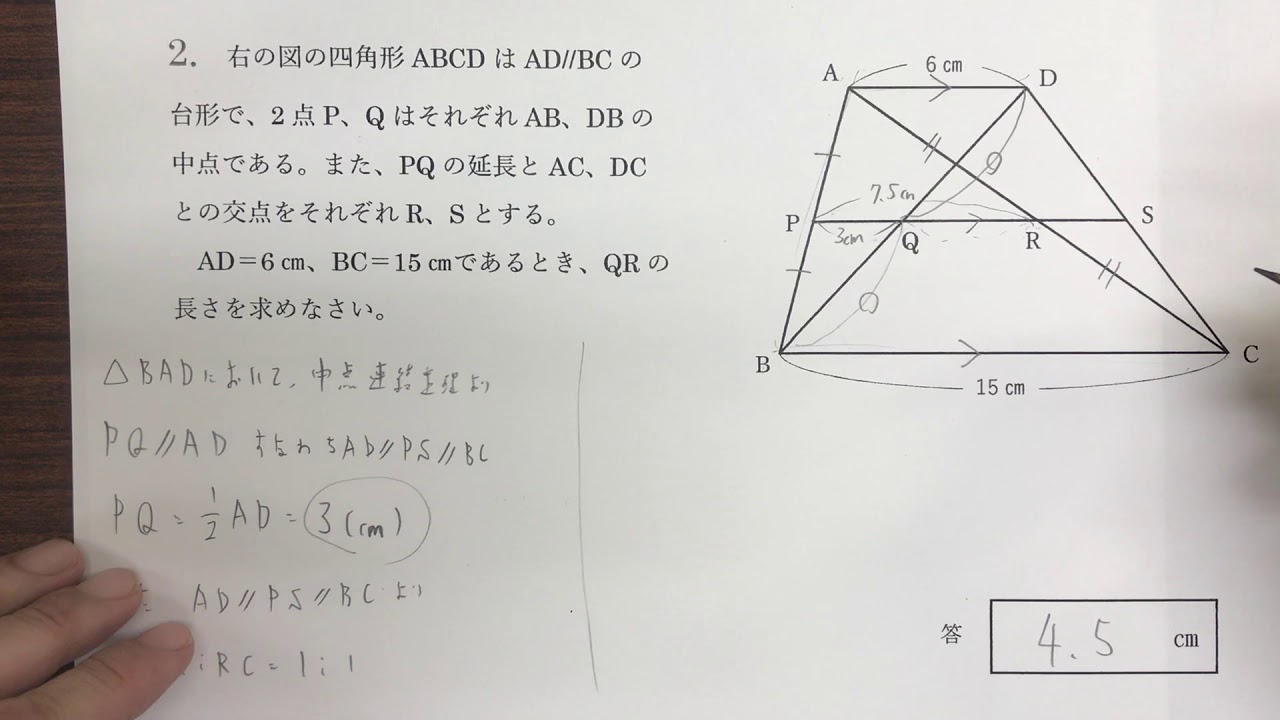



図形 証明 応用問題 相似中心 大問2 中学数学単元別強化教材 これから 図形 紹介動画 3年生2学期レベル Youtube
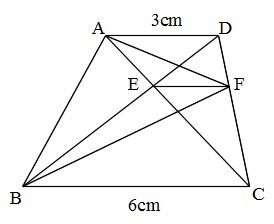
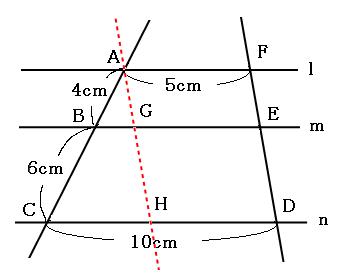
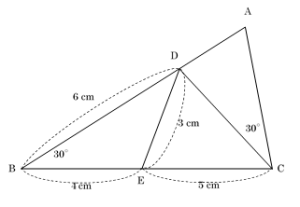
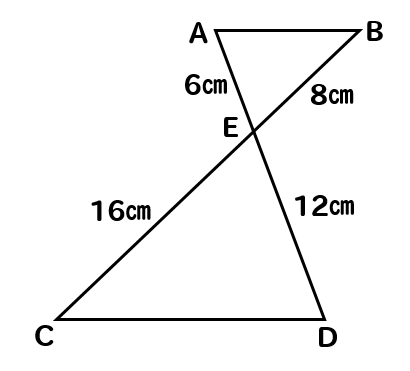
空間図形 相似な立体では 長さの比は相似比と同じ。 面積比は相似比の2乗。 体積比は相似比の3乗。 相似比がabの相似な図形の場合 辺、高さなど 長さの比は a b 表面積など 面積比は a 2 b 2 体積比は a 3 b 3 例 相似比23の相似な円柱PとQがある。 2h 2r 3r 3h相似図形については,3組の辺の比が等しくなる. ⇒ この公式を使って辺の長さを求めることができる. ABDC=AEDE=BECE が成り立つ. もちろん, これは辺の長さが BE=3 とか CE=2 などということではない .比が 32 ということは,実際の長さとしては 6 と 4中学受験では三角形の相似のほとんどが、 「対応する2つの角が等しい三角形は相似」 という相似条件になっていますから、 まずは 「角の大きさ」に着目する ように促してあげましょう。 もうひとつの「ミス」は、 面積比の問題で「相似比と面積比の関係」と




相似な図形 三角形の相似条件 中学数学 By となりがトトロ マナペディア



中学数学 図形の相似
・ あ 、 い 、( あ い )、3つの直角三角形が相似 ・相似比よりも「直角三角形の3辺比」を使うことが多い a:b:c = m:x:a = x:n:b ・m:n = あ :い = (a×a):(b×b) 理由 あ と い は相似比a:bより、面積比(a×a):(b×b)相似な図形 北上市立上野中学校 平成27年10月 1日 281 jhsu 中 3 数学 相似な図形 相似な図形の面積と体積 滝沢市立滝沢中学校 平成27年10月29日 280 jhsu 中 3 数学 相似な図形 二戸市立浄法寺中学校 平成27年11月12日 279 jhsu 中 3 数学 三平方の定理次に 色々な図形を例に、相似形に拡大・縮小したり、縦・横に拡大・縮小する場合の手順を以下に説明します。 ⅰ)相似形に拡大・縮小する 相似形に拡大・縮小する時は、編集ハンドルの四隅の を使います。 此処では楕円を例に説明します。
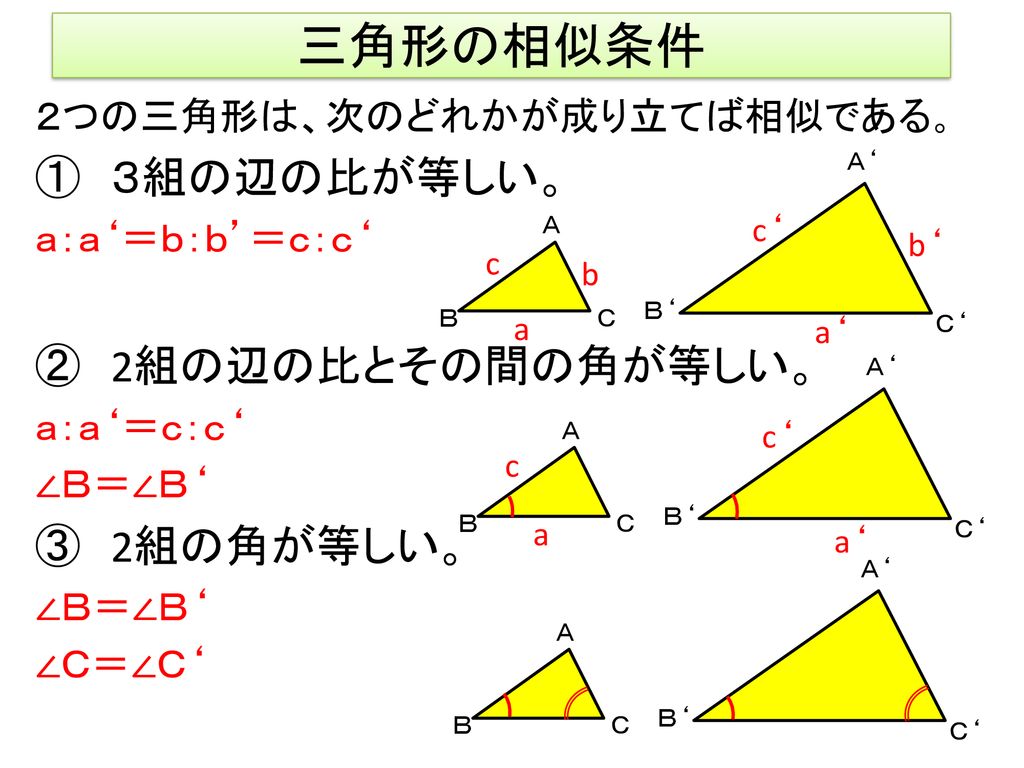



本時のねらい 図形の中から相似な三角形を見出し 相似条件を用いて証明することができる Ppt Download




中学数学 相似な図形の面積比 中学数学の無料オンライン学習サイトchu Su
中3数学「図形と相似」がわからない人は、以下の順でTry ITの映像授業を観て勉強してみてください。 「図形の相似」に関する6のポイントを覚える 「平行線と線分の比」に関する7のポイントを覚える 「相似な図形の面積と体積」に関する3のポイントを覚える まずはこれらのポイントをしっかり覚えてから、練習や例題にある問題を解いて「図形と相似」のわから 図形・相似 拡大、縮小の関係を相似といいます。 三角形が相似かどうか、という相似条件の暗記と、 その証明も含みます。 ここも慣れが重要です。 入試直前期にはじめてこの単元を学習するのではなく、夏休みくらいには学習を済ませておきたい単元です。 はじめに 本記事では、「相似とは?」「合同と何が違うの?」「相似の記号って?」という基本的な質問から、三角形の相似条件や相似比の使い方などの実戦的な内容まで解説しています。 高校受験を控えた中学三年生にとって、「相似」は非常に難しい単元です。 その分受験生との差が開きやすく、志望高校合格を左右することもあります。 また、大学入試問題で




図形と相似 Qikeru 学びを楽しくわかりやすく



子どもを混乱させる相似な三角形の2つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生
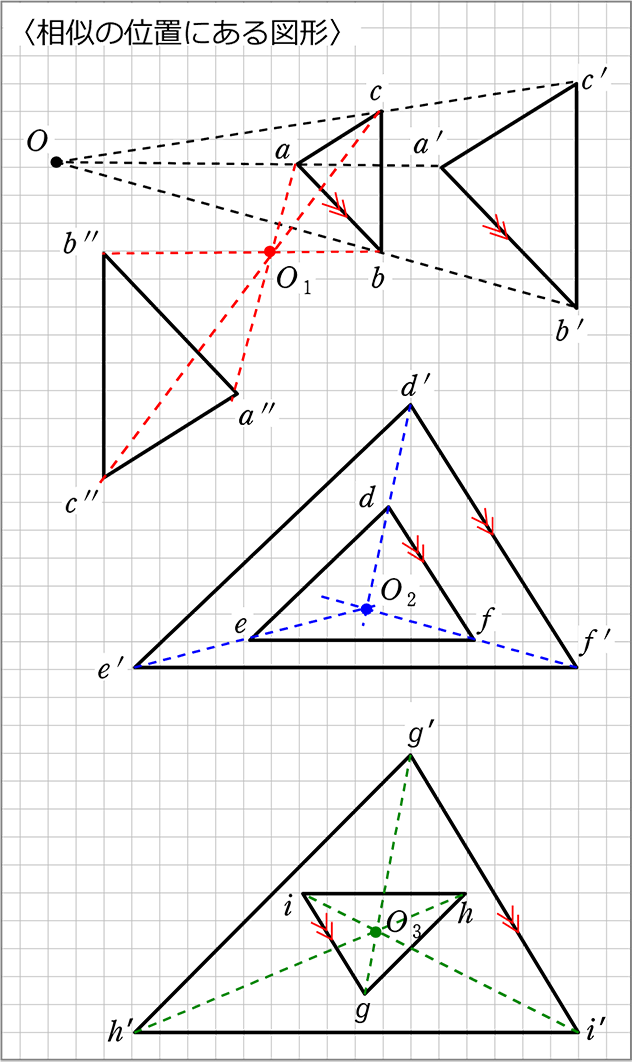
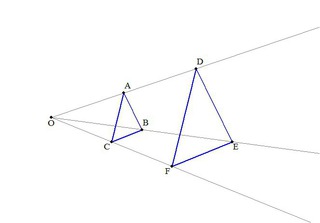
また、教科書108ページの図形を比べて、同じ形で2倍の図形になってるか確認する。 拡大、縮小及び拡大図、縮図について確認する。 2つの図形があって、一方の図形を拡大または縮小したものと、他方の図形が合同であるとき、この2つの図形は相似で・拡大、縮小、相似の意味がわかる。 ・相似の位置、相似の中心の意味を理解し、相似の中心を求めることができる。 ・拡大または縮少した図形をかいて、相似な図形の性質を考えることができる。 ⑤使用機材 定規、OHP Çe ÿ 0N{IeY ²{,ÿ f^tepfyÑc\ hH今回は、中3で学習する 『相似な図形』の単元の中から 平行線と線分の比という内容について解説してきます。 ここでは、相似な図形の性質をつかって いろんな図形の辺の長さを求めていきます。 長々と解説をするよりも 問題を見ながら、実践を通して学習するのが良いので いろんな問題を解きながら解説をしていきます。 今回解説していく問題はこちら!




面積比の公式まとめ 相似比と面積比と体積比の関係もあわせて解説 遊ぶ数学



相似とは 三角形の相似条件 記号 相似比 面積比 証明問題 受験辞典
相似記号の左右の図形が相似であることを示す。 一般には2次元の図形に対して用いるが、3次元以上の場合にもこの記号が用いられる。 使用例 abc ∽ def (三角形abcと三角形defが相似である) 字形に相似比の意味と比の性質を利用 表現・処理 ☆図を通して、視覚的にとらえやすい学習プリント 相似な図形の性質を使っ して、相似な図形の辺の長さを求 相似な図形の性質を使 を用意する。 て対応する辺の長さを求 め、その求め方を説明してみよう。




数学 最重要 高さ共通 と 相似 面積比 集中特訓 2 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




中3 数学相似まとめてみた 中学生 数学のノート Clear




三角形の面積比と相似比 チーム エン




中3数学 相似の証明問題 練習編 映像授業のtry It トライイット
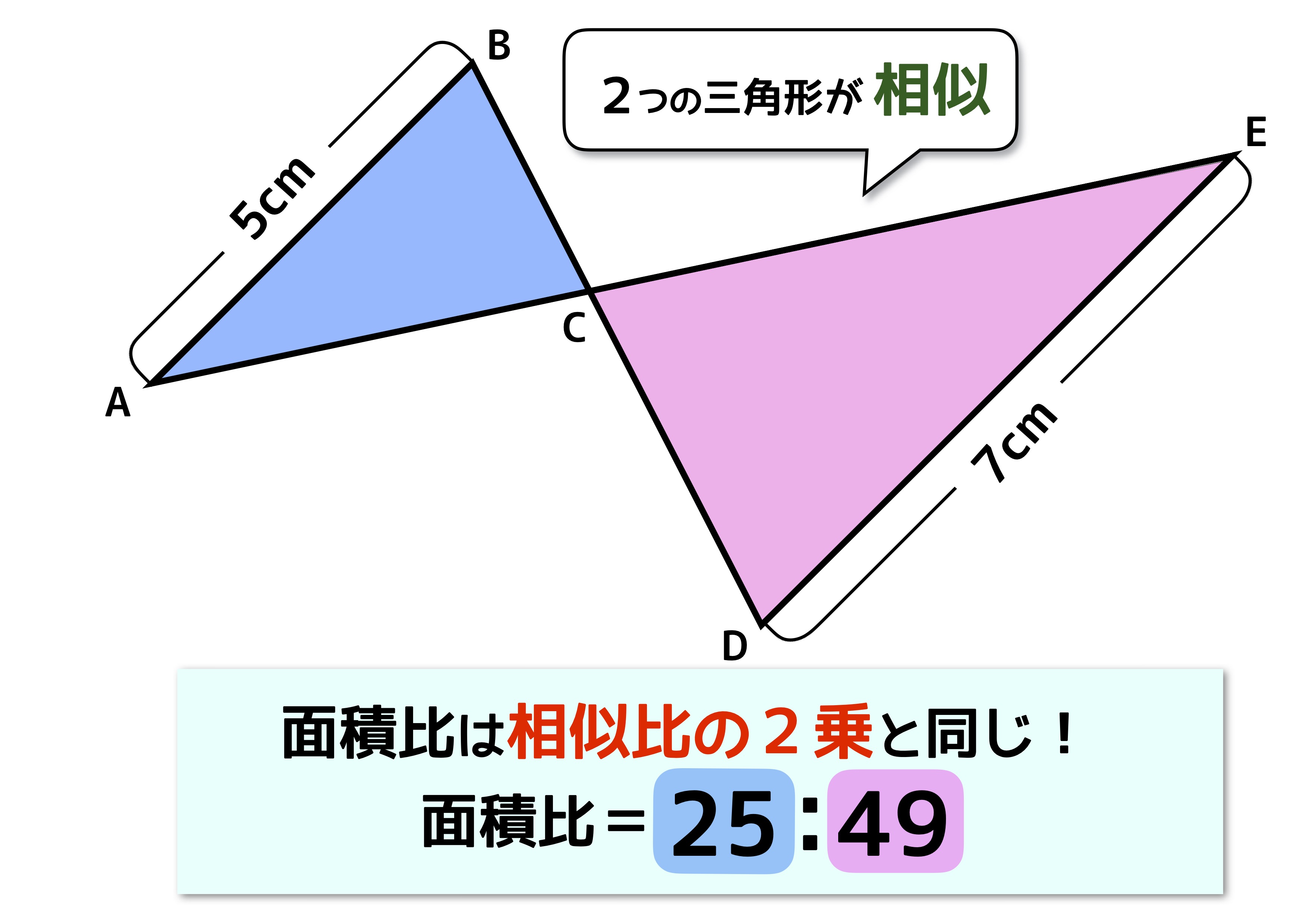



中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ




相似な図形 補助線を引いて考える相似の問題 中学生からの質問 数学 進研ゼミ中学講座 中ゼミ
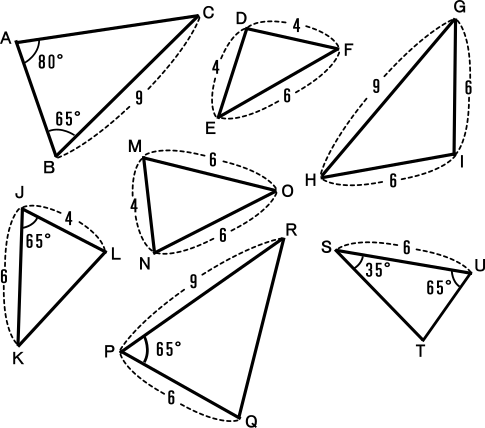



中学3年数学練習問題 三角形の相似条件の問題




中3数学 図形と相似9 相似条件と証明 折り返しの図形 すべて無料 星組の中学数学講座




難関中学に合格する 相似形と面積比 図形の移動トレーニング 改訂4版 Yell Books Amazon Com Books



相似とは何か その意味 合同との違い 相似な図形が持つ性質について アタリマエ



中学数学 相似とは何か 導入 中学数学の無料オンライン学習サイトchu Su



Homeroom 数学の入試問題を解くとき大切なこと 正しい入り口から入らないと問題は解けない 平面図形 相似 働きアリ
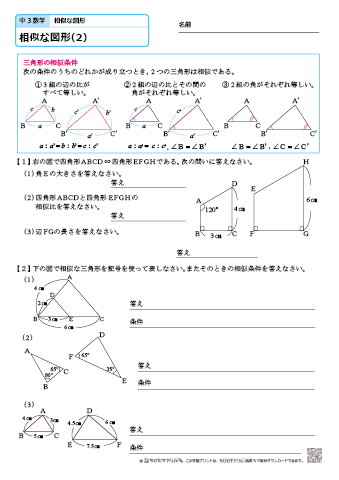



中学3年生 数学 相似な図形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中学3年数学練習問題 図形と相似の定期テスト対策問題
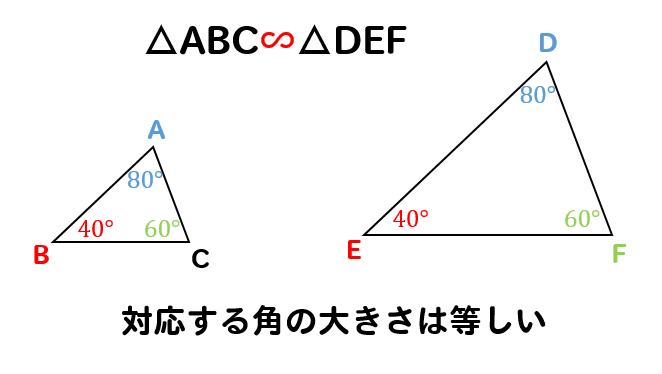



中3数学 相似の基本性質をわかりやすく問題解説 数スタ




相似な図形の面積比の問題について質問です Clear




中3数学 図形と相似27 相似な図形の面積比 すべて無料 星組の中学数学講座
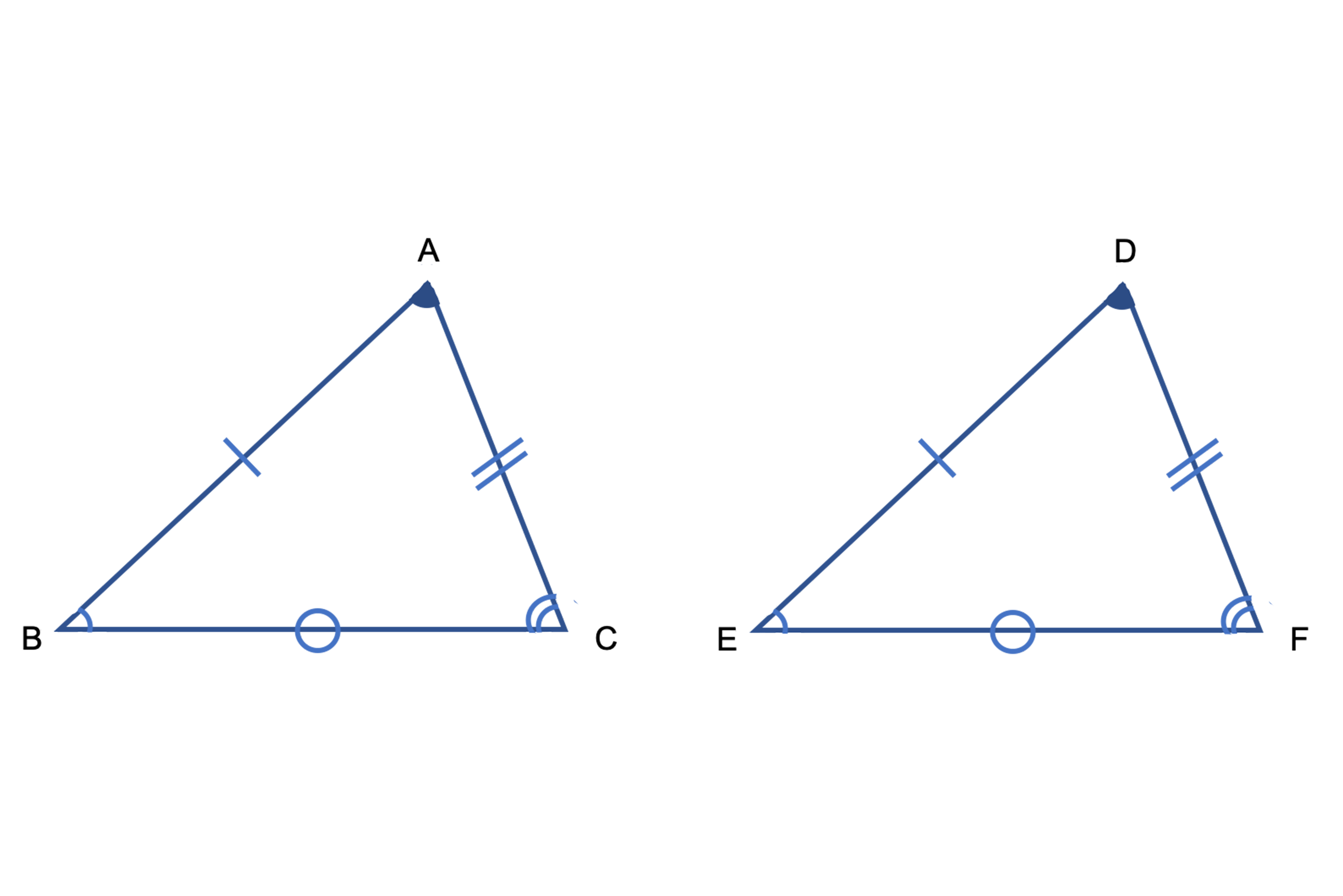



記号にすると と 三角形の 合同 と 相似 の違いをまとめよう 受験に関する豆知識 学習塾ランキング検索総合サイト 塾プラス
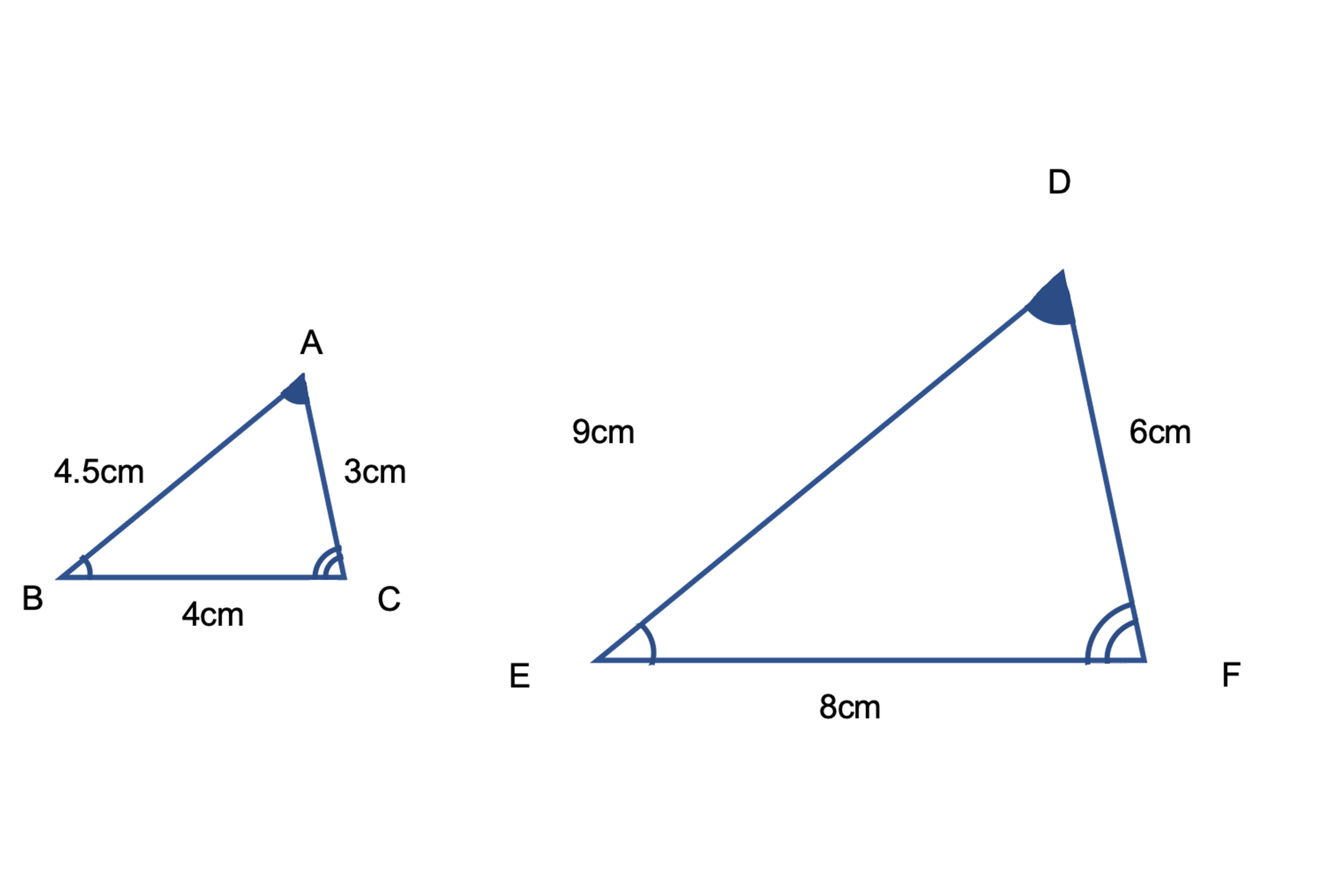



記号にすると と 三角形の 合同 と 相似 の違いをまとめよう 受験に関する豆知識 学習塾ランキング検索総合サイト 塾プラス



U9j580gf8iba369ji2w Xyz P 1096
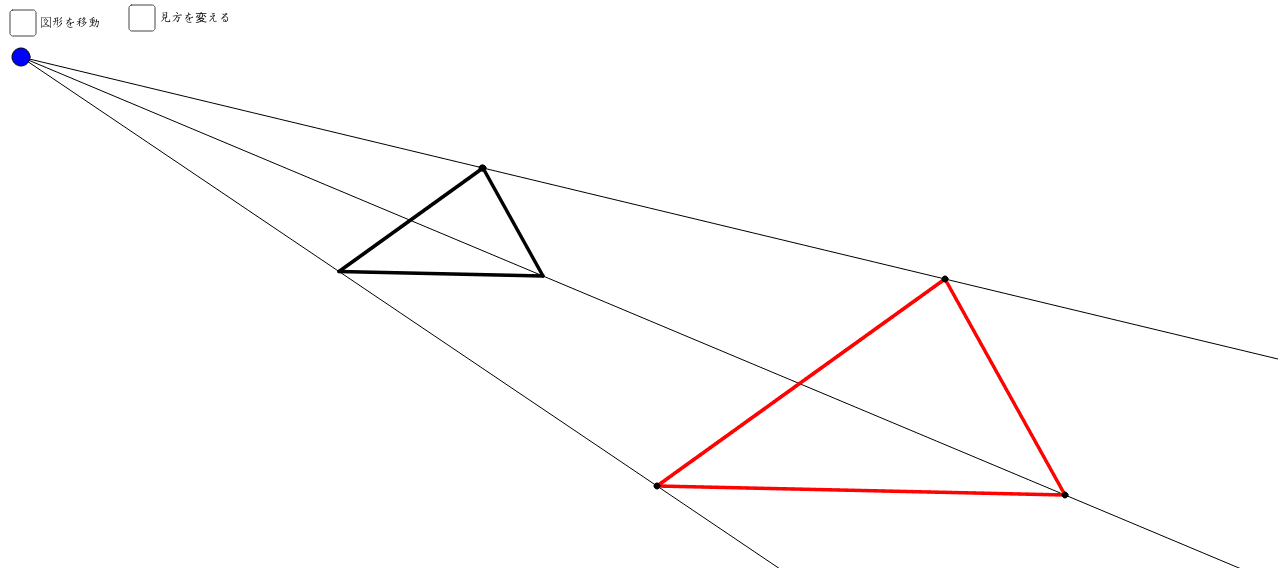



相似な図形の特徴 Geogebra
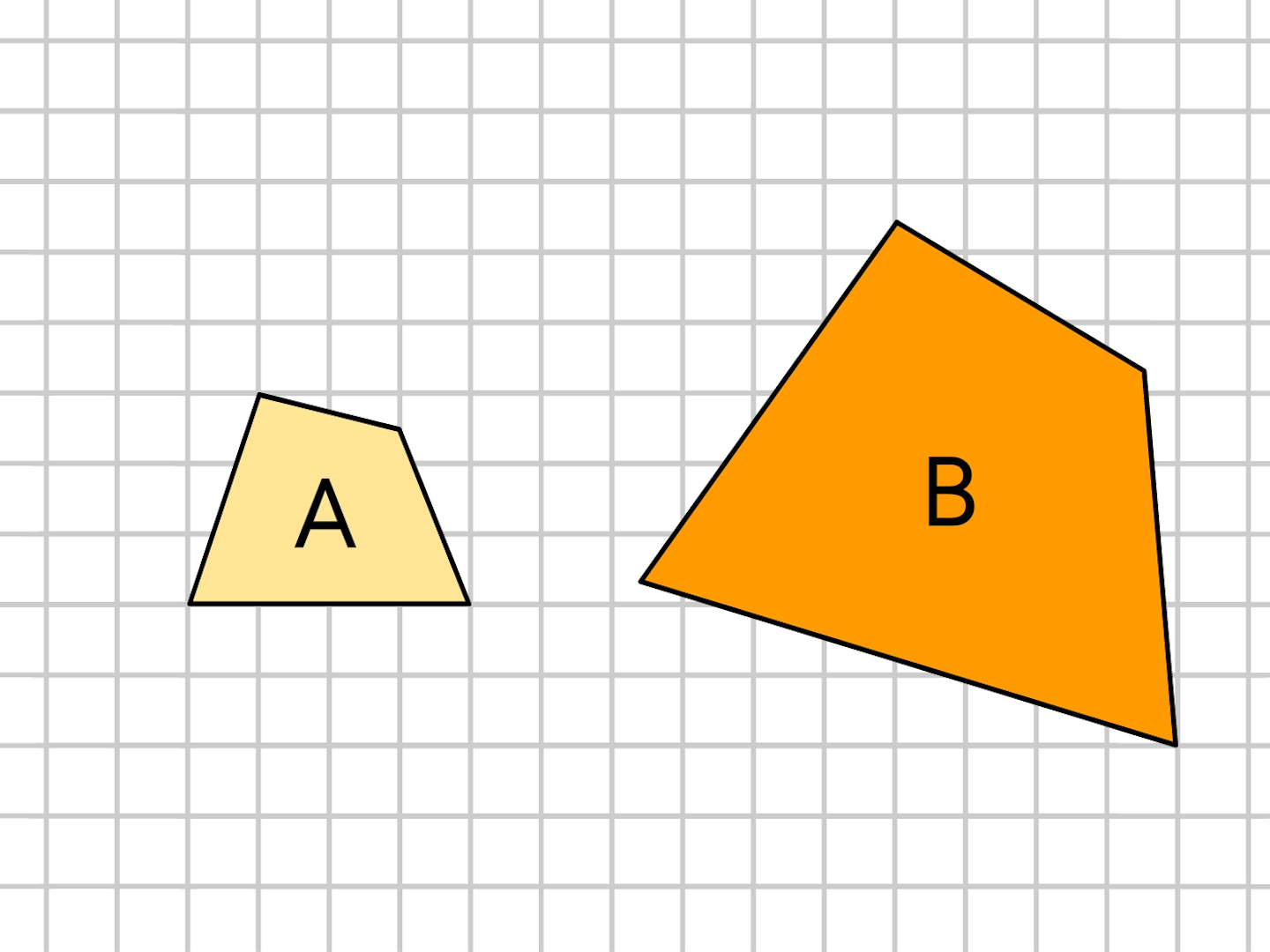



3年 相似な図形とその性質 数学イメージ動画集 大日本図書



中学3年数学図形と相似解説をお願いします 正五角形abcdeの各頂点を結んでで Yahoo 知恵袋




開成中学入試問題 算数 を徹底解説 平成29年度 算数 大問3 1 相似の図形ー第2回 星一徹式ゲリラ中学受験
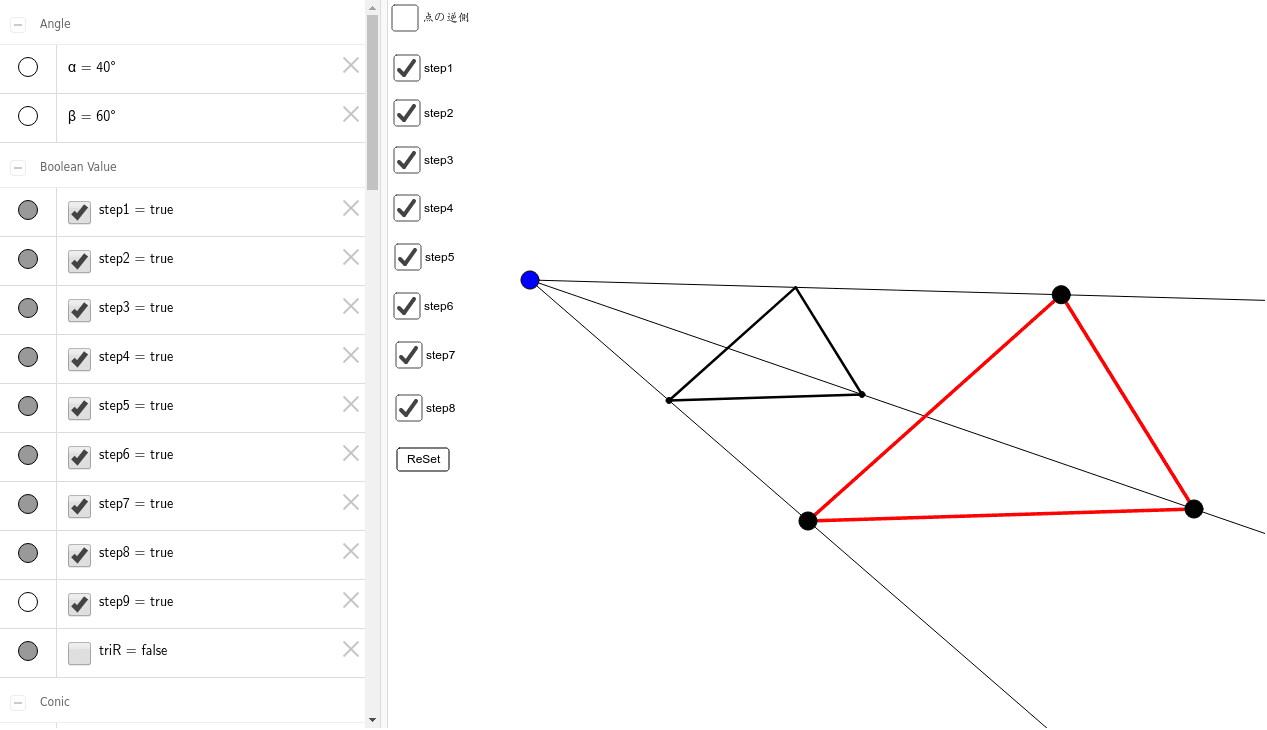



相似な図形の特徴 Geogebra
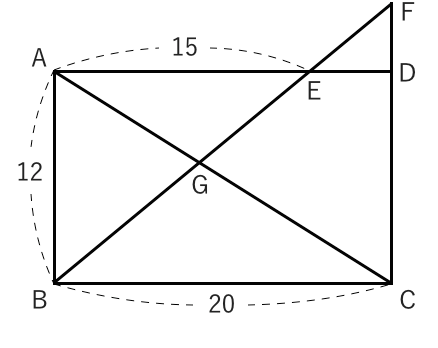



相似な図形 面積比の問題 苦手な数学を簡単に




Math 相似 相似の難問を ちょうちょ と おむすび で簡単に解く 1 働きアリ



相似 三角形の相似条件 記号や証明問題も Studyplus スタディプラス
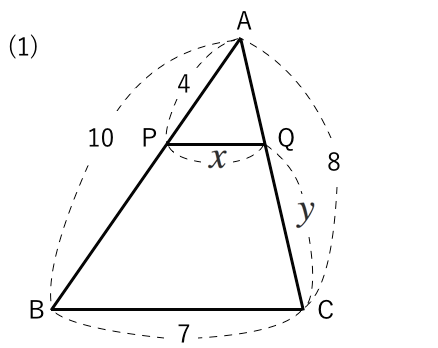



相似な図形 長さを求める 苦手な数学を簡単に



相似比



相似比とは 1分でわかる意味 面積比 四角形と三角形の問題



Math 空間図形と相似 面積比 体積比 発展問題 働きアリ
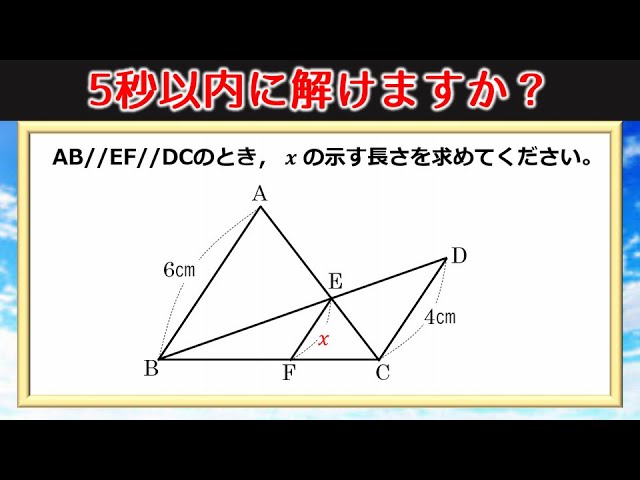



図形問題 知っている人は5秒で解ける相似の裏技 Youtube



Studydoctor相似な図形や中心の作図 中3数学 Studydoctor



Q Tbn And9gcqxcmz5ohxoigvlvb2w1anis4ck46lrpvf7degdyd8ydfuomdi1 Usqp Cau




ม 3 โน ตของ 数学 相似な図形 授業ノート ช น Junior Clear




相似な図形 しっしーのお計算ん向上委員会
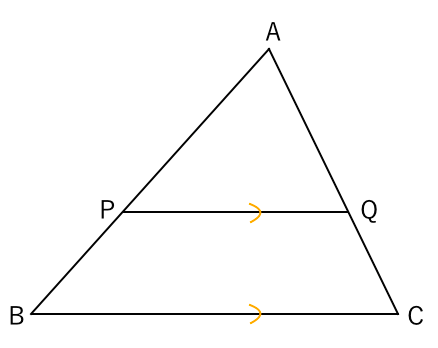



相似な図形 計算について覚えること 苦手な数学を簡単に
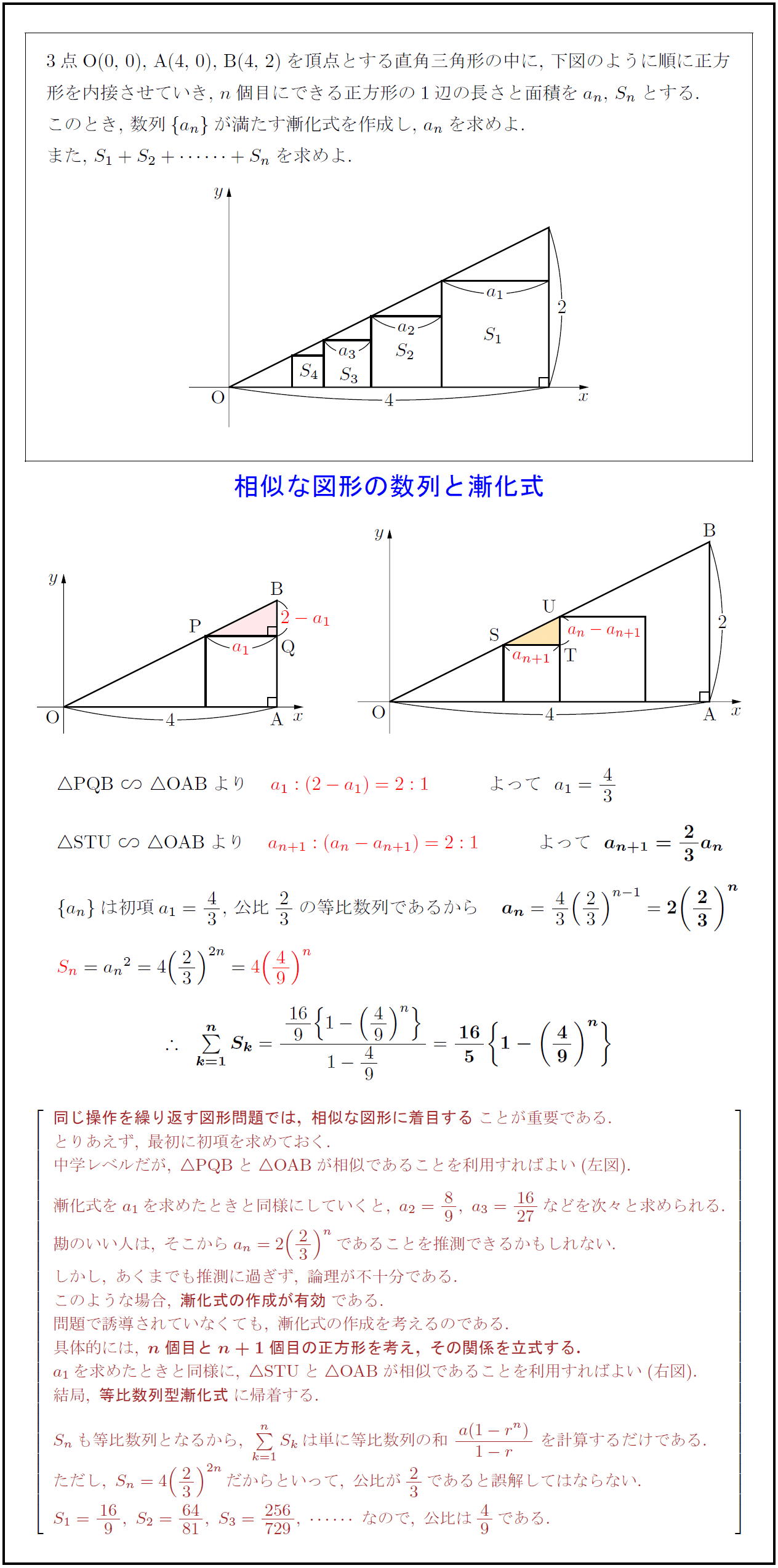



高校数学b 相似な図形の数列と漸化式 受験の月
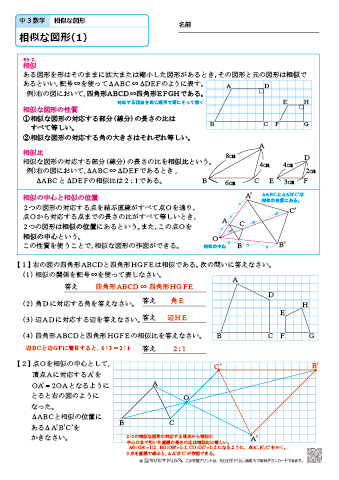



中学3年生 数学 相似な図形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中3数学 図形と相似31 相似な図形の面積比 すべて無料 星組の中学数学講座




図形の相似 Similarity Geometry Japaneseclass Jp
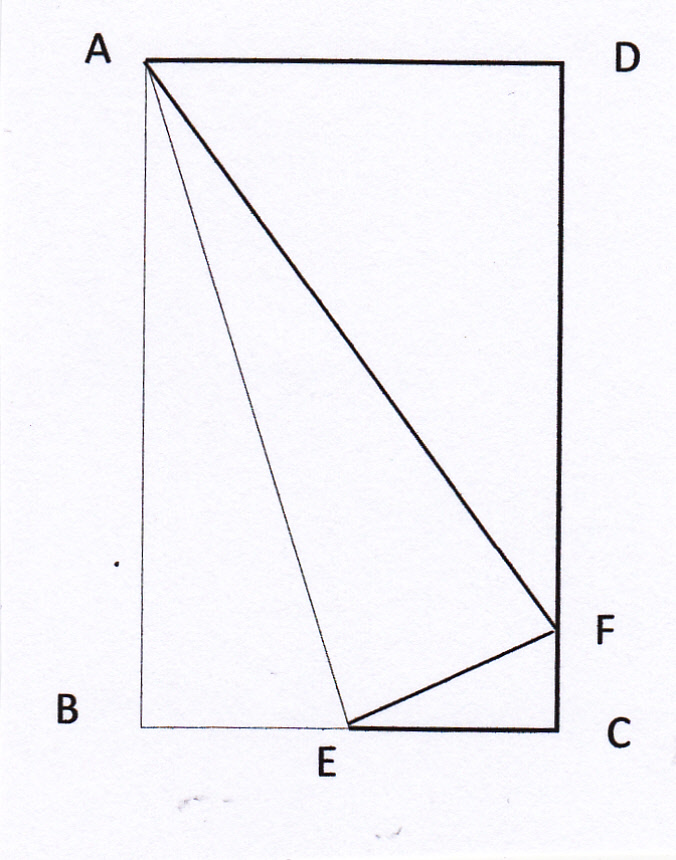



図形の折り返しと三角形の相似の証明 解き方 現役塾講師のわかりやすい中学数学の解き方



1
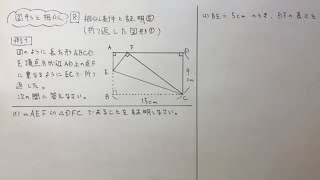



中3数学 図形と相似8 相似条件と証明 折り返した図形 すべて無料 星組の中学数学講座




中三受験講座 英数ポイント解説映像授業 進研ゼミ中学講座会員サイト
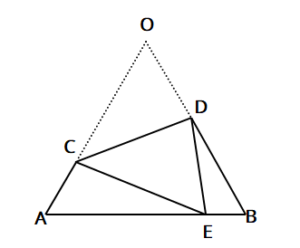



高校入試対策数学 折り返し図形と相似の融合問題 中学生勉強サイトあかね先生
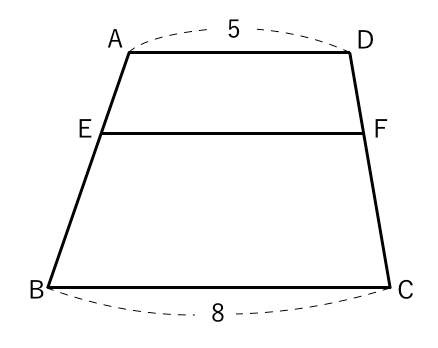



相似な図形 計算 台形 練習問題 苦手な数学を簡単に
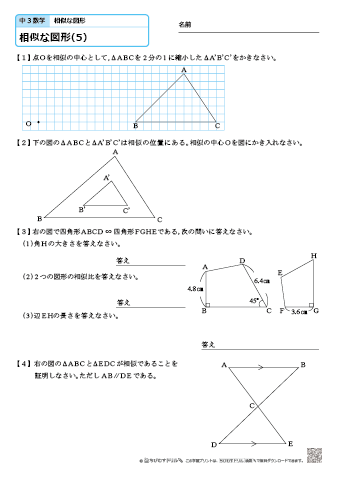



中学3年生 数学 相似な図形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




世界一わかりやすい数学問題集中3 5章 図形と相似




初等数学模索生活 相似な図形 1




中3数学 相似 1 相似な図形 相似条件 Ex 1 Youtube




3分でわかる 相似比から面積比の公式 Qikeru 学びを楽しくわかりやすく




中3 相似の問題です 相似な図形の対応順が問題によってはわからな 数学 教えて Goo



相似な図形の問題の解き方を解説 相似は隠れたチョウチョとトンガリを探すべし




無料 中3数学 標準問題 解答プリント 328 図形の相似3 線分の比
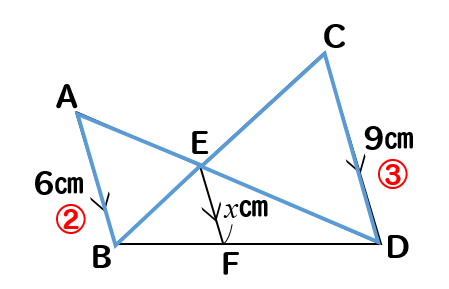



相似 平行線と比の利用 辺の長さを求める方法をまとめて問題解説 数スタ
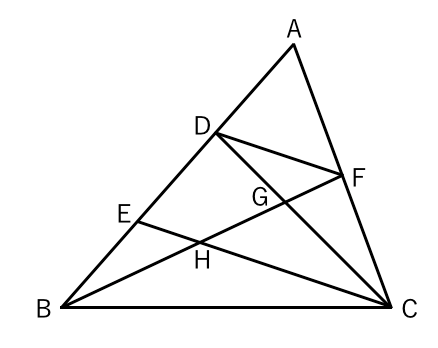



相似な図形 平行線と線分の比 よく出る系 苦手な数学を簡単に



相似な図形 おやじさん ネット



相似な図形 三角形の相似条件 相似比 勉強ナビゲーター




世界一わかりやすい数学問題集中3 5章 図形と相似



中学校数学 3年生 図形 相似な図形 Wikibooks



高校入試 英語 数学 図形と相似 相似の基礎




中3 相似な図形 中学生 数学のノート Clear



中3数学 覚えて損はない 相似な図形の性質2つ Qikeru 学びを楽しくわかりやすく




中3 数学 中3 相似な図形 中学生 数学のノート Clear
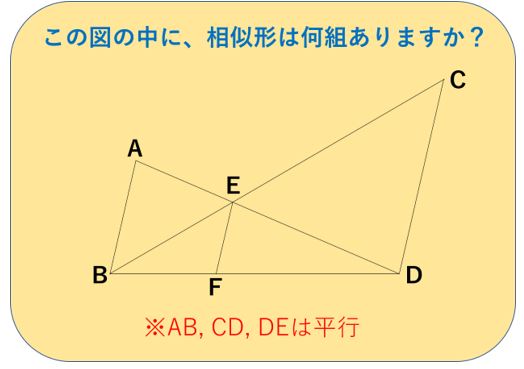



平面図形と比 相似形を探してみよう 中学受験プロ講師ブログ



すぐるゼミ 相似な図形の応用



中3数学 相似な図形の見つけ方 相似条件とは 基本問題を使って解説 数スタ




相似な図形の面積比 Youtube



中3数学 覚えて損はない 相似な図形の性質2つ Qikeru 学びを楽しくわかりやすく



相似と相似の条件を知ろう 数学の要点まとめ 練習問題一覧




図形と相似 1 きっずゼミ子育て応援ブログ




問題2の 2 について質問です なぜ 相似な図形の面積の比であるのに Clear




図形と相似 の勉強法のわからないを5分で解決 映像授業のtry It トライイット




図形と相似 2 きっずゼミ子育て応援ブログ




世界一わかりやすい数学問題集中3 5章 図形と相似




図形の相似 の問題のわからないを5分で解決 映像授業のtry It トライイット



図形の相似 規則集3 中学から数学だいすき



Http Www Pref Chiba Lg Jp Kyouiku Shidou Gakuryoku Yaruki Suugaku Documents M3012 Pdf



相似な図形 ピンポイント計算式 苦手な数学を簡単に




図形の相似 の問題のわからないを5分で解決 映像授業のtry It トライイット



Q Tbn And9gcte8fsqvrlckxdilyd5wnblxavnplfa7mg7ddvhyyrzhuvjel Usqp Cau




中学3年 数学 東京書籍 新しい数学 相似な図形 平行線と比 赤城 ᐡᐤᐡ



相似を見つけよう 平面図形 パズル おもしろ算数問題




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ




中学数学の三角形の相似 相似条件 図形の証明と相似比 面積比 リョースケ大学
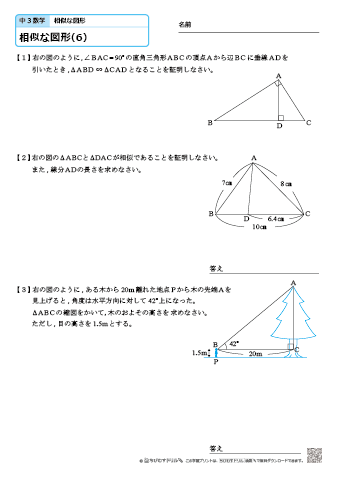



中学3年生 数学 相似な図形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




相似な図形 はこれでカンペキ 相似な図形のかき方8種類 算数を究める




中3数学 図形と相似23 平行線と線分の比 比の合成 連比 すべて無料 星組の中学数学講座



0 件のコメント:
コメントを投稿